Question

The figure below shows a combination of capacitors. Find (a) the equivalent capacitance of combination, and (b) the energy stored in C3 and C4.

Answer 1

A) C_{eq} = 15 10⁻⁶ F, B) U₃ = 3 J, U₄ = 0.5 J

Step-by-step explanation:

In a complicated circuit, the method of solving them is to work the circuit in pairs, finding the equivalent capacitance to reduce the circuit to simpler forms.

In this case let's start by finding the equivalent capacitance.

A) Let's solve the part where C1 and C3 are. These two capacitors are in serious

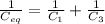`(1)/(C_(eq)) = (1)/(C_1) + (1)/(C_3)` (you has an mistake in the formula)

`(1)/(C_(eq1)) = ((1)/(30) + (1)/(15)) \ 10^(6)`

`(1)/(C_(eq1))` = 0.1 10⁶

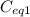`C_(eq1)` = 10 10⁻⁶ F

capacitors C₂, C₄ and C₅ are in series

`(1)/(C_(eq2)) = (1)/(C_2) + (1)/(C_4) + (1)/(C_5)`

`(1)/(C_(eq2) ) = ((1)/(15) + (1)/(30) + (1)/(10) ) \ 10^6`

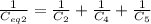
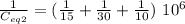
`(1)/(C_(eq2) )` = 0.2 10⁶

`C_(eq2)` = 5 10⁻⁶ F

the two equivalent capacitors are in parallel therefore

C_{eq} = C_{eq1} + C_{eq2}

C_{eq} = (10 + 5) 10⁻⁶

C_{eq} = 15 10⁻⁶ F

B) the energy stored in C₃

The charge on the parallel voltage is constant

is the sum of the charge on each branch

Q = C_{eq} V

Q = 15 10⁻⁶ 6

Q = 90 10⁻⁶ C

the charge on each branch is

Q₁ = Ceq1 V

Q₁ = 10 10⁻⁶ 6

Q₁ = 60 10⁻⁶ C

Q₂ = C_{eq2} V

Q₂ = 5 10⁻⁶ 6

Q₂ = 30 10⁻⁶ C

now let's analyze the load on each branch

Branch C₁ and C₃

In series combination the charge is constant Q = Q₁ = Q₃

U₃ =
`(Q^2)/(2 C_3)`

U₃ =
`( 60 \ 10^(-6))/(2 \ 10 \ 10^(-6))`

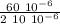
U₃ = 3 J

In Branch C₂, C₄, C₅

since the capacitors are in series the charge is constant Q = Q₂ = Q₄ = Q₅

U₄ =
`(30 \ 10^(-6))/( 2 \ 30 \ 10^(-6))`

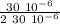
U₄ = 0.5 J