Given:
The cost function is:
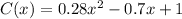
where C(x) is the cost per hour in millions of dollars and x is the number of items produced per hour in thousands.
To find:
The minimum production cost.
Solution:
We have,
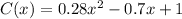
It is a quadratic function with positive leading efficient. It means it is an upward parabola and its vertex is the point of minima.
If a quadratic function is
 , then the vertex of the parabola is:
, then the vertex of the parabola is:
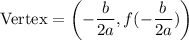
In the given function,
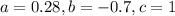 . So,
. So,

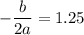
Putting
 in the given function to find the minimum production cost.
in the given function to find the minimum production cost.
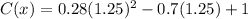
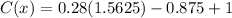
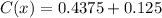
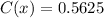
Therefore, the minimum production cost is 0.5625 million dollars.