Answer:
ΔR = 9 s
Step-by-step explanation:
To calculate the propagation of the uncertainty or absolute error, the variation with each parameter must be calculated and the but of the cases must be found, which is done by taking the absolute value
The given expression is R = 2A / B
the uncertainty is ΔR = |
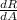 | ΔA + |
| ΔA + |
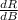 | ΔB
| ΔB
we look for the derivatives
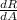 = 9 / B
= 9 / B
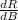 = 9A (
= 9A (
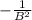 )
)
we substitute
ΔR =
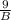 ΔA +
ΔA +
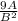 ΔB
ΔB
the values are
ΔA = 2 s
ΔB = 3 s
ΔR =
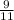 2 +
2 +
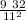 3
3
ΔR = 1.636 + 7.14
ΔR = 8,776 s
the absolute error must be given with a significant figure
ΔR = 9 s