Answer with explanation:
*Pre-condition: The mass of all blocks are evenly distributed.
As you add more and more blocks, the center of mass of the system changes.
Let the first block be the support. The maximum distance that can be unsupported (hung over) by the second block is equal to half the length of second block.
Why?
Let's take a look at our formula for torque. Torque,
 , is given by:
, is given by:
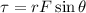 , where
, where
 is radius,
is radius,
 is force, and
is force, and
 is the angle between the radius and level arm.
is the angle between the radius and level arm.
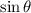 is used to calculate the relevant component of a force producing torque. In this case, the only force acting on the object is the force of gravity. Therefore,
is used to calculate the relevant component of a force producing torque. In this case, the only force acting on the object is the force of gravity. Therefore,
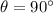 and recall
and recall
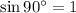 .
.
Conceptually, it's more important to look at the
 term here. From our formula, we can see that if
term here. From our formula, we can see that if
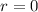 , there is no torque.
, there is no torque.
The point of pivot will be at the center of mass. Here's the important part:
As long as the point of pivot is supported,
 will remain zero and no torque will be created from the force of gravity. As you keep stacking blocks, as long as the center of mass of the entire system remains supported from your first support, the tower will not fall.
will remain zero and no torque will be created from the force of gravity. As you keep stacking blocks, as long as the center of mass of the entire system remains supported from your first support, the tower will not fall.
In the given picture shown, that first block will be your support.
The 6 blocks on top of that first block form a center of mass that is still on that first block, thus allowing the tower to remain standing.