Question

Second time I’ve posted this. Please help!! :)

Answer 1

-2 is an extraneous solution because it creates 0 in the denominator.

There is one acceptable solution to the equation

Explanation:

x² + 5x + 6 = x² + 2x + 3x + 6

= x(x + 2) + 3(x + 2)

= (x + 2)(x + 3)

`(x)/(x+2)+(2)/(x^(2)+5x+6)=(5)/((x+3))\\\\(x)/(x+2)+(2)/((x+2)(x+3))=(5)/((x+3))\\\\(x*(x+3))/((x+2)(x+3))+(2)/((x+2)(x+3))=(5*(x+2))/((x+3)(x+2))\\\\(x^(2)+3x+2)/((x+2)(x+3))=(5x+10)/((x+3)(x+2))\\\\`

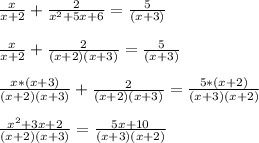
x² + 3x + 2 = 5x + 10

x² + 3x - 5x + 2 - 10 = 0

x² - 2x - 8 = 0

x² + 2x - 4x - 8 = 0

x(x + 2) - 4(x + 2) = 0

(x + 2)(x - 4) = 0

x +2 = 0 or x - 4 = 0

x = - 2 or x = 4