Question

The function f(x) = log4x is dilated to become g(x) = f (1/3x).
What is the effect on f(x)?

Answer 1

Given:

The functions are:

`f(x)=\log_4x`

`g(x)=f\left((1)/(3)x\right)`

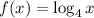
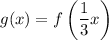
The function f(x) is dilated to become g(x).

To find:

The effect on f(x).

Solution:

Transformation is defined as:

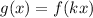`g(x)=f(kx)` ...(i)

Where, k is the factor of horizontal stretch and compression.

If 0<k<1, then the graph of f(x) stretched horizontally by factor
`(1)/(k)`.

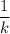If k>1, then the graph of f(x) compressed horizontally by factor
`(1)/(k)`.

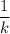It is given that

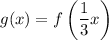`g(x)=f\left((1)/(3)x\right)` ...(ii)

On comparing (i) and (ii), we get

`k=(1)/(3)`

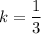
Therefore, the graph of f(x) stretched horizontally by factor
`3`.