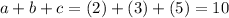Answer:
Explanation:
We are given that the graph of the equation:
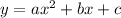
Passes through the three points (0, 5), (1, 10), and (2, 19).
And we want to find the value of (a + b + c).
First, since the graph passes through (0, 5), its y-intercept or c is 5. Hence:
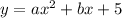
Next, since the graph passes through (1, 10), when x = 1, y = 10. Substitute:
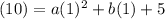
Simplify:
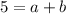
The point (2, 19) tells us that when x = 2, y = 19. Substitute:
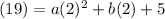
Simplify:
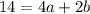
This yields a system of equations:
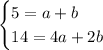
Solve the system. We can do so using elimination (or any other method you prefer). Multiply the first equation by negative two:
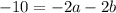
Add the two equations together:
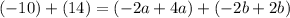
Combine like terms:
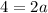
Hence:
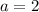
Using the first equation:
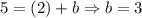
Therefore, our equation is:
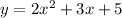
Thus, the value of (a + b + c) will be: