9514 1404 393
Answer:
(2x -4) +1/(x -2) -2/(x +4)
Explanation:
The attached shows the quotient is (2x -4) and the remainder expressed as a fraction is ...
r = (8 -x)/(x^2 +2x -8)
So, the problem is to write the partial fraction expansion of this remainder. It will be of the form ...
r = A/(x -2) +B/(x +4)
where (x-2)(x+4) is the factorization of the divisor quadratic.
The value of A can be found by evaluating (x -2)r at x=2.
(x -2)r for x=2 is (8 -2)/(2 +4) = 6/6 = 1
The value of B can be found by evaluating (x +4)r at x=-4.
(8 -(-4))/(-4-2) = 12/-6 = -2
Then the quotient and remainder, written as partial fractions is ...
= (2x -4) +1/(x -2) -2/(x +4)
_____
Additional comment
In the form ...

we can see that (x -2)r will be ...
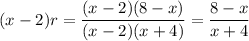
This can be evaluated at x=2, as we have done above. Similar factor cancellation works to give (x+4)r = (8-x)/(x-2).
This method of arriving at the "A" and "B" values may not pass technical scrutiny regarding where r is defined or undefined--but it works. One could consider the work to be finding a limit, rather than evaluating a rational function at points where it is undefined.