Question

It's camping season! Ernie and Bert set up their tents 15 m from

each other. Ernie has Tent 1 and Bert has Tent 2. The angle
between the line of sight from Bert's tent to the shower and the
line of sight from Bert's tent to Ernie's tent is 78 degrees. If
Ernie's tent is 19m away from the shower, is Bert 's tent closer or
further away from the shower and by how much? In your
calculations, round your angles to the nearest whole degree and
side measurements to the nearest tenth of a metre.
1
2

Answer 1

The answer is "21.6".

Explanation:

Let A stand for tent 1

Let B stand for tent 2

Let C be a shower

Using cosine formula:

`c= √(b^2 +a^2 - 2ab\cdot \cos(C))\\\\`

`= \sqrt{(19)^2 + (15)^2 - 2\cdot 19 \cdot 15 \cdot \cos(78^(\circ))}\\\\= \sqrt{361 + 225 - 570\cdot \cos(78^(\circ))}\\\\ = \sqrt{586- 570\cdot \cos(78^(\circ))}\\\\= 21.6\\\\`

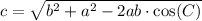
Therefore, you need to reduce the similarity from B to C which is the length from tent 2 to shower:

Tent 2 Distance to Dusk = 21.6m

Bert's tent is 21.6m away from the shower