Question

Rationalize the denominator of $\displaystyle \frac{1}{\sqrt{2} + \sqrt{3} + \sqrt{7}}$, and write your answer in the form\[

\frac{A\sqrt{2} + B\sqrt{3} + C\sqrt{7} + D\sqrt{E}}{F},
\]where everything is in simplest radical form and the fraction is in lowest terms, and $F$ is positive. What is $A + B + C + D + E + F$?

Answer 1

9514 1404 393

Answer:

57

Explanation:

Apparently, you want to simplify ...

`\displaystyle (1)/(√(2) + √(3) + √(7))`

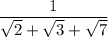
so the denominator is rational. It looks like the form you want is ...

`(A√(2) + B√(3) + C√(7) + D√(E))/(F)`

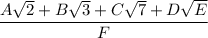
And you want to know the sum A+B+C+D+E+F.

__

We can start by multiplying numerator and denominator by a conjugate of the denominator. Then we can multiply numerator and denominator by a conjugate of the resulting denominator.

`\displaystyle =(1)/(√(2) + √(3) + √(7))\cdot(√(2) + √(3) - √(7))/(√(2) + √(3) - √(7))=(√(2) + √(3) - √(7))/(2√(6)-2)\\\\=(√(2) + √(3) - √(7))/(2√(6)-2)\cdot(√(6)+1)/(√(6)+1)=((1+√(6))(√(2)+√(3)-√(7)))/(10)\\\\=(√(2)+√(3)-√(7)+2√(3)+3√(2)-√(42))/(10)=(4√(2)+3√(3)-√(7)-√(42))/(10)`

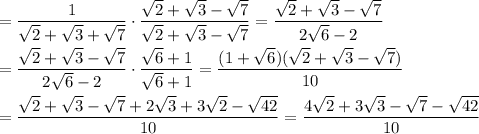
Comparing this to the desired form we have ...

A = 4, B = 3, C = -1, D = -1, E = 42, F = 10

Then the sum is ...

A +B +C +D +E +F = 4 + 3 -1 -1 +42 +10 = 59 -2 = 57

The sum of interest is 57.