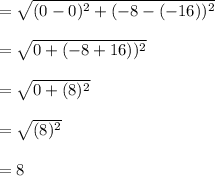Answer:
Following are the responses to the given question:
Explanation:
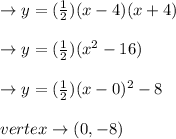
The general x-intercept parabola equation
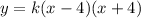
Parabola crosses the dot (2,-12)
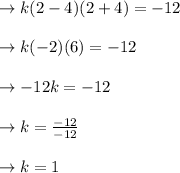
The parabolic equation which crosses the position
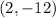 is
is
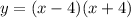
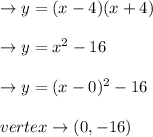
The distance among the vertices of the two parabolas: