Answer:
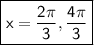
Explanation:
A trigonometric equation is given to us , and we need to find the solutions of the equation within the interval [ 0,2π ]
The given equation is ,
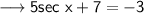
Add -7 to both sides ,
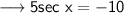
Divide both sides by 5 ,

Simplify ,
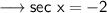
Now solve for x ,
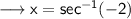
Simplify ,
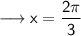
The secant function is negative in the second and third quadrants. Subtracting the reference angle from 2π to find the solution in the third quadrant to find the solution second solution.

Simplify ,

Now here the period of sec x is 2π . Therefore ,
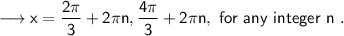
Therefore all the possible solutions are ,
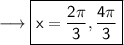
Hence the required answer is 2π/3 and 4π/3.