Answer:
f = 106.3 N
Step-by-step explanation:
The force applied on the sled must be equal to the static frictional force to move the sled:
Tension Force Horizontal Component = Static Frictional Force
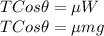
where,
T = Tension = 120 N
θ = angle of rope = 37°
μ = coefficient of static friction = ?
m = mass of children plus sled = 55 kg
g = acceleration due to gravity = 9.81 m/s²
Therefore,
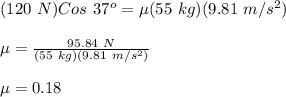
Now, the static friction acting on the mother will be:
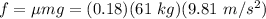
f = 106.3 N