Question

Instructions: Find the lengths of the other two sides of the isosceles right triangle below.

Answer 1

Given:

The ratio of 45-45-90 triangle is
`x:x:x√(2)`.

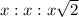The hypotenuse of the given isosceles right triangle is
`7√(2)`.

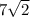To find:

The lengths of the other two sides of the given isosceles right triangle.

Solution:

Let
`l` be the lengths of the other two sides of the given isosceles right triangle.

From the given information if is clear that he ratio of equal side and hypotenuse is
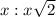`x:x√(2)`. So,

`(x)/(x√(2))=(l)/(7√(2))`

`(1)/(√(2))=(l)/(7√(2))`

`(7√(2))/(√(2))=l`

`7=l`

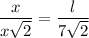
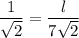
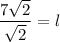
Therefore, the lengths of the other two sides of the given isosceles right triangle are 7 units.