Question

Which of the following is the maximum value of the function y = −x^2 + 2x + 1?

Answer 1

Explanation:

We don't need choices to find out the correct answer. Solve this problem by completing the square. Begin by setting the quadratic equal to 0 and moving over the constant, like this:

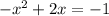`-x^2+2x=-1` and factor out the -1 in front of the x-squared, since the leading coefficient HAS to be a 1:

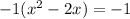`-1(x^2-2x)=-1` Now take half the linear term, square it, and add it to both sides. Our linear term is -2. Half of -2 is -1, and squaring that gives us 1. So we add a 1 into both sides. But that -1 out front there on the left is a multiplier, so what we actually added in was -1(1) which is -1:

`-1(x^2-2x+1)=-1-1`

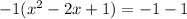
On the left side we have a perfect square binomial, which is why we do this, and on the right side we have -2:

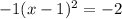`-1(x-1)^2=-2` and we can move that constant back over and set the quadratic back equal to y:

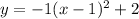`y=-1(x-1)^2+2` which gives us a max height of 2.

(If this was modeling parabolic motion, we would know that the time it takes to get to that max height is 1 second. The vertex of this parabola is (1, 2))