Question

Steel rods are manufactured with a mean length of 29 centimeter (cm). Because of variability in the manufacturing process, the lengths of the rods are approximately normally distributed with a standard deviation of 0.07 cm. (a) What proportion of rods has a length less than 28.9 cm? (b) b) Any rods that are shorter than 24.84 cm or longer than 25.16 cm are discarded. What proportion of rods will be discarded?

Answer 1

Given data :

The mean length of the steel rod = 29 centimeter (cm)

The standard deviation of a normally distributed lengths of rods = 0.07 centimeter (cm)

a). We are required to find the proportion of rod that have a length of less than 28.9 centimeter (cm).

Therefore, P(x < 28.9) = P(z < (28.9-29) / 0.07)

= P(z < -1.42)

= 0.0778

b). Any rods which is shorter than
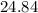`24.84` cm or longer than
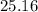`25.16` cm that re discarded.

Therefore,

P (x < 24.84 or 25.16 < x) = P( -59.42 < z or -54.85)

= 1.052