Answer:
1. a) x1 = -8 y x2 = -4
b) x1 = -1/3
2. a) x1 = 0 y x2 = -5
b) x1 = 4 y x2 = -4
3. m debe ser 6. Asi tendriamos (x+3)²=0
4. a) x1 = 4, x2 = -4, x3 = 3 y x3 = -3
b) x1 = 3, x2 = -3 las otras dos raices son complejas.
Explanation:
1. a)
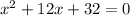
Factorizando:
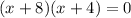
Entonces: x1 = -8 y x2 = -4
4. a) x1 = 4, x2 = -4, x3 = 3 y x3 = -3
b)
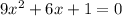
Factorizando:
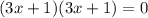
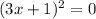
Entonces: x1 = -1/3
2. a)
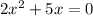
Aplicando factor comun:
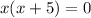
Entonces: x1 = 0 y x2 = -5
b)
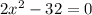
Despejamos x.
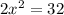
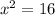
Entonces: x1 = 4 y x2 = -4
3. m debe ser 6. Asi tendriamos (x+3)²=0
4. a)
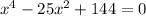
Hacemos cambio de variable:
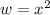
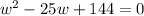
Ahara podemos factorizar:
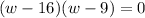
Usando el cambio de variable nuevamente.
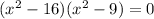
Entonces los valores de x son: x1 = 4, x2 = -4, x3 = 3 y x3 = -3
b)
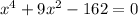
Hacemos cambio de variable:
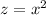
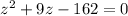
Ahara podemos factorizar:
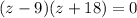
Usando el cambio de variable nuevamente.
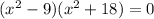
Entonces los valores de x son: x1 = 3, x2 = -3 las otras dos raices son complejas.
Espero ye haya servido!