Given:
The different recursive formulae.
To find:
The explicit formulae for the given recursive formulae.
Solution:
The recursive formula of an arithmetic sequence is
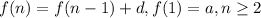 and the explicit formula is
and the explicit formula is
 , where a is the first term and d is the common difference.
, where a is the first term and d is the common difference.
The recursive formula of a geometric sequence is
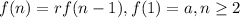 and the explicit formula is
and the explicit formula is
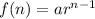 , where a is the first term and r is the common ratio.
, where a is the first term and r is the common ratio.
The first recursive formula is:
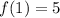
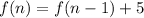 for
for
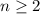 .
.
It is the recursive formula of an arithmetic sequence with first term 5 and common difference 5. So, the explicit formula for this recursive formula is:
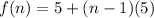
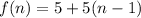
Therefore, the correct option is A, i.e.,
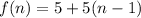 .
.
The second recursive formula is:
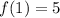
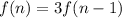 for
for
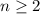 .
.
It is the recursive formula of a geometric sequence with first term 5 and common ratio 3. So, the explicit formula for this recursive formula is:
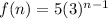
Therefore, the correct option is F, i.e.,
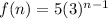 .
.
The third recursive formula is:
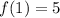
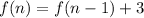 for
for
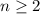 .
.
It is the recursive formula of an arithmetic sequence with first term 5 and common difference 3. So, the explicit formula for this recursive formula is:
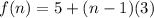
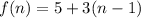
Therefore, the correct option is D, i.e.,
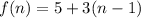 .
.