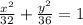Question

This ellipse is centered at the

origin. Find its equation.
Vertices: (0,-6) and (0,6)
Foci: (0,-2) and (0,2)
y?
X^2/[?] + y^2/[?] =1

Answer 1

Equation of Ellipse is
`(x^(2) )/(32) +(y^(2) )/(36) =1`

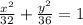
Explanation:

Let's find the value for
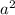`a^(2)` and
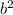`b^(2)` to write the equation for vertical ellipse.

Here 'a' is the distance from center to one of the vertices.

"b" is the distance from center to one of the Co-vertices. We need to find this using formula
`a^(2) -b^(2) =c^(2)`

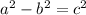
'c' is the distance between center to one of the Foci.

In this problem center is origin.

So, a =6(because distance between(0,0) and (0,6) is 6)

c= 2 (because distance between (0,0) and (0,2) is 2)

Plug in the known values into the formula
`a^(2) -b^(2) =c^(2)`

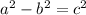
36-
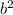`b^(2)`= 4

Subtract both sides 36

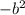`-b^(2)` = -32

Divide both sides by -1

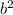`b^(2)` =32

So, equation would be

`(x^(2) )/(32) +(y^(2) )/(36) =1`