Question

asked Feb 3, 2022 68.1k views

1 Answer

Cristian Contrera · Answer 1 · 2022-02-09T05:26:42+0000

Answer:

0.50 or about half a year longer.

Explanation:

We can write an equation to model bot investments.

Oliver invested $970 in an account paying an interest rate of 7.5% compounded continuously.

Recall that continuous compound is given by the equation:

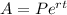
A = Pe^(rt)

Where A is the amount afterwards, P is the principal amount, r is the rate, and t is the time in years.

Since the initial investment is $970 at a rate of 7.5%:

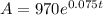
A = 970e^(0.075t)

Carson invested $970 in an account paying an interest rate of 7.375% compounded annually.

Recall that compound interest is given by the equation:

$\displaystyle A = P\left(1+(r)/(n)\right)^(nt)$

Where A is the amount afterwards, P is the principal amount, r is the rate, n is the number of times compounded per year, and t is the time in years.

Since the initial investment is $970 at a rate of 7.375% compounded annually:

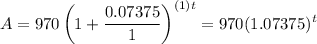
$\displaystyle A = 970\left(1+(0.07375)/(1)\right)^((1)t)=970(1.07375)^t$

When Oliver's money doubles, he will have $1,940 afterwards. Hence:

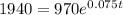
1940= 970e^(0.075t)

Solve for t:

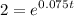
$\displaystyle 2 = e^(0.075t)$

Take the natural log of both sides:

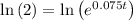
$\ln\left (2\right) = \ln\left(e^(0.075t)\right)$

Simplify:

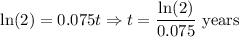
$\ln(2) = 0.075t\Rightarrow \displaystyle t = (\ln(2))/(0.075)\text{ years}$

When Carson's money doubles, he will have $1,940 afterwards. Hence:

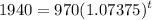
$\displaystyle 1940=970(1.07375)^t$

Solve for t:

2=(1.07375)^t

Take the natural log of both sides:

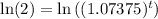
$\ln(2)=\ln\left((1.07375)^t\right)$

Simplify:

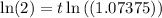
$\ln(2)=t\ln\left((1.07375)\right)$

Hence:

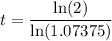
$\displaystyle t = (\ln(2))/(\ln(1.07375))$

Then it will take Carson's money:

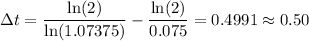
$\displaystyle \Delta t = (\ln(2))/(\ln(1.07375))-(\ln(2))/(0.075)=0.4991\approx 0.50$

About 0.50 or half a year longer to double than Oliver's money.

Please log in or register to add a comment.