Given:
your speed = 70 mph
Your friend's speed = 75 mph
You want to drive at least 500 miles per day.
You also plan to spend no more than 10 hours driving each day.
To find:
The system of linear inequalities that represents this situation.
Solution:
Let x be the number of hours you drive and let y represents the number of hours your friend will drive.
You also plan to spend no more than 10 hours driving each day.
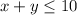
Your speed is 70 mph and your friend's speed is 75 mph. So, the distance covered in x and y hours are 70x miles and 75y miles respectively.
You want to drive at least 500 miles per day. So, the total distance must be greater than or equal to 500.
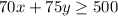
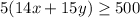
Divide both sides by 5.
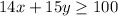
Therefore, the required system of inequalities has two inequalities
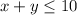 and
and
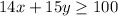 .
.