Answer:
B) 399
Explanation:
We want to find the sum of the arithmetic series given that:
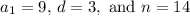
In other words, we want to find the sum of the first 14 terms of the series when the first term is 9 and the common difference is 3.
Recall that the sum of an arithmetic series is given by:
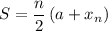
Where n is the amount of terms, a is the first term, and xₙ is the nth or last term.
We will need to find the last term. We can write a direct formula. The general form of a direct formula is given by:
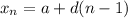
Since the initial term is 9 and the common difference is 3:
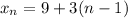
Then the 14th or last term is:

Then the sum of the first 14 terms is:
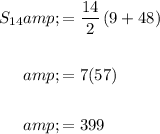
Our answer is B.