Question

Please help!!!!!! 50 points!!

Answer 1

26

Explanation:

we want to figure out the area of the composite figure notice that the composite figure contains three rectangles therefore in order to find the area of the composite figure we need find the area of the rectangles first

finding the area of the first & last rectangles:

the first and last rectangles are congruent therefore they will have the same area thus

`\displaystyle A _( \rm 1)rect) = A _( \rm 3)rect) = l * w`

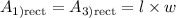
from the figure we obtain:

• 
  `l = 5`
• 
  `w = 2`

thus substitute:

`\displaystyle A _( \rm 1)rect) = A _( \rm 3)rect) = 5* 2`

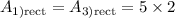
simplify multiplication:

`\displaystyle A _( \rm 1)rect) = A _( \rm 3)rect) = 10`

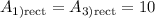
finding the area of the middle rectangle:

the middle rectangle has a length and width of 3 and 2 respectively Thus

`\displaystyle A _( \rm 2)rect) =3 * 2`

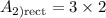
simplify multiplication:

`\displaystyle A _( \rm 2)rect) =6`

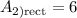
finding the area of the composite figure:

`\rm \displaystyle A _( \rm composite) = A _( \rm 1)rect) + A _( \rm 2)rect) + A _( \rm 3)rect)`

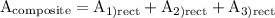
substitute what we got:

`\rm \displaystyle A _( \rm composite) = 10 + 6 + 10`

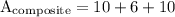
simplify addition:

`\rm \displaystyle A _( \rm composite) = \boxed{ 26}`

hence,

the answer is 26 square units

Answer 2

Area of first rectangle= 5×2=10units

Area of second rectangle= 3×2= 6 units

Area of third rectangle = 5×2= 10 units

Now,

Total area of figure = 10+6+10= 26units✓