Question

Each side of a square is increasing at a rate of 8 cm/s. At what rate (in cm2/s) is the area of the square increasing when the area of the square is 49 cm2

Answer 1

The surface area of a square of side L is given by

`A = L^2`

The rate of change of the area per unit time is

`(dA)/(dt) = 2L(dL)/(dt)`

We can express the length L on the right hand side in terms of the area A
`(L = √(A))`:

`(dA)/(dt) = 2√(A)(dL)/(dt)`

`\:\:\:\:\:\:\:=2(\sqrt{49\:\text{cm}^2})(8\:\text{cm/s})`

`\:\:\:\:\:\:\:=112\:\text{cm}^2\text{/s}`

Answer 2

Explanation:

This is nice and simple. I'm going to walk through it like I do when teaching this concept to my class for the first time. This is a good problem for that.

We are given a square and we are looking for the rate at which the area is increasing when a certain set of specifics are given. That means that the main equation for this problem is the area of a square, which is:

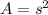`A=s^2` where s is a side.

Since we are looking for the rate at which the area is changing,
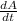`(dA)/(dt)`, we need to take the derivative of area formula implicitly:

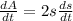`(dA)/(dt)=2s(ds)/(dt)` that means that if
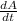`(dA)/(dt)` is our unknown, we need values for everything else. We are given that the initial area for the square is 49. That will help us determine what the "s" in our derivative is. We plug in 49 for A and solve:

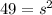`49=s^2` so

s = 7

We are also given at the start that the sides of this square are increasing at a rate of 8cm/s. That is
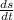`(ds)/(dt)`. Filling it all in:

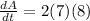`(dA)/(dt)=2(7)(8)` and

`(dA)/(dt)=112(cm^2)/(s)`