Question

The surface area of a melting snowball decreases at a rate of3.8cm2/min. Find the rate at which its diameter decreases when the diameter is13cm. (Round your answer to three decimal places if required)

Answer 1

Explanation:

This is a pretty basic related rates problem. I'm going to go through this just like I do in class when I'm teaching it to my students.

We see we have a snowball, which is a sphere. We are talking about the surface area of this sphere which has a formula of

`S=4\pi r^2`

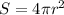
In the problem we are given diameter, not radius. What we know about the relationship between a radius and a diameter is that

d = 2r so

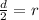`(d)/(2)=r` Now we can have the equation in terms of diameter instead of radius. Rewriting:

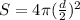`S=4\pi((d)/(2))^2` which simplifies to

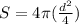`S=4\pi((d^2)/(4))` and a bit more to

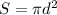`S=\pi d^2` (the 4's cancel out by division). Now that is a simple equation for which we have to find the derivative with respect to time.

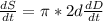`(dS)/(dt)=\pi*2d(dD)/(dt)` Now let's look at the problem and see what we are given as far as information.

The rate at which the surface area changes is -3.8, and we are looking for
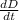`(dD)/(dt)`, the rate at which the diameter is changing, when the diameter is 13. Filling in:

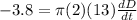`-3.8=\pi(2)(13)(dD)/(dt)` and solving for the rate at which the diameter is changing:

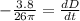`-(3.8)/(26\pi)=(dD)/(dt)` and divide to get

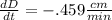`(dD)/(dt)=-.459(cm)/(min)` Obviously, the negative means that the diameter is decreasing.