The question is incomplete. The complete question is :
You would like to have enough money saved to receive a growing annuity for 25 years, growing at a rate of 4 percent per year, with the first payment of $60,000 occurring exactly one year after retirement. How much would you need to save in your retirement fund to achieve this goal? (The interest rate is 12%.)
Solution :
Given data :
pv of growing annuity, i = 0.04
Rate of interest, r = 0.12
Therefore,


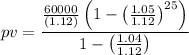
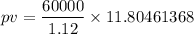
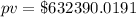
pv = $ 632390.02 (rounding off)