Answer:
The answer is
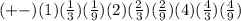
Step-by-step explanation:
Rational root theorem, also called rational root test, in algebra, theorem that for a polynomial equation in one variable with integer coefficients to have a solution (root) that is a rational number, the leading coefficient (the coefficient of the highest power) must be divisible by the denominator of the fraction and
and the constant term (the one without a variable) must be divisible by the numerator.
In f(x), the ratio is

because 4 is the constant and 9 is leading term
So our factors are
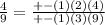
If