Question

A 4.17 L volume of oxygen gas measured at 7.62 °C is expanded to a new volume of 4.50 L. Calculate the temperature (in oC) of the gas at the higher volume, assuming no change in pressure.

Answer 1

`\boxed {\boxed {\sf 8.22 \ \textdegree C}}`

Step-by-step explanation:

The question asks us to calculate the temperature of the gas at the higher volume. Since the pressure is constant, we are only concerned about volume and temperature. We will use Charles's Law. This states that the volume of a gas and the temperature of the gas have a directly proportionate relationship. The formula is:

`\frac {V_1}{T_1}= (V_2)/(T_2)`

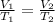
The gas starts at a volume of 4.17 liters and a temperature of 7.62 degrees Celsius.

`\frac {4.17 \ L}{7.62 \textdegree C} = (V_2)/(T_2)`

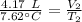
The gas is expanded to a new volume of 4.50 liters, but the temperature is unknown.

`\frac {4.17 \ L}{7.62 \textdegree C} = (4.50 \ L)/(T_2)`

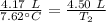
We want to solve for the temperature at a higher volume. We must isolate the variable T₂. Cross multiply. Multiply the first numerator and second denominator, then the first denominator and second numerator.

`4.17 \ L * T_2 = 4.50 \ L * 7.62 \textdegree C`

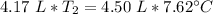
The variable is being multiplied by 4.17 liters. The inverse of multiplication is division. Divide both sides by 4.17 L.

`\frac {4.17 \ L * T_2 }{4.17 \ L}= (4.50 \ L * 7.62 \textdegree C)/(4.17 \ L)`

`T_2=(4.50 \ L * 7.62 \textdegree C)/(4.17 \ L)`

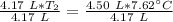
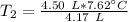
The units of liters (L) cancel.

`T_2=(4.50 * 7.62 \textdegree C)/(4.17 )`

`T_2=(34.29)/(4.17 ) \textdegree C`

`T_2=8.22302158273 \textdegree C`

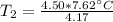
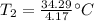
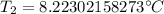
The original measurements of liters and temperature have 3 significant figures, so our answer must have the same. For the number we calculated, that is the hundredth place.

The 3 to the right in the thousandth place tells us to leave the 2 in the hundredth place.

`T_2 \approx 8.22 \ \textdegree C`

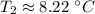
The temperature of the gas at the higher volume is approximately 8.22 degrees Celsius.