Question

Given: APRS, RS=10
mZP=45º, mzS=600
Find: Perimeter of APRS

Answer 1

Perimeter of ΔPRS = 35.91 units

Explanation:

From the figure attached,

By applying triangle sum theorem in the given triangle PRS,

m∠P + m∠R + m∠S = 180°

45° + m∠R + 60° = 180°

m∠R = 75°

By applying sine rule,

`\frac{\text{sinP}}{RS}= \frac{\text{sinS}}{PR}=\frac{\text{sinR}}{PS}`

`\frac{\text{sin}(45^(\circ))}{10}= \frac{\text{sin}(60^(\circ))}{PR}=\frac{\text{sin}(75^(\circ))}{PS}`

`\frac{\text{sin}(45^(\circ))}{10}= \frac{\text{sin}(60^(\circ))}{PR}`

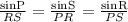
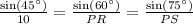
PR = 12.25 units

`\frac{\text{sin}(45^(\circ))}{10}=\frac{\text{sin}(75^(\circ))}{PS}`

PS = 13.66 units

Perimeter of triangle PRS = PR + PS + RS

= 12.25 + 13.66 + 10

= 35.91