Answer:

Step-by-step explanation:
We are asked to find the pressure given a change in volume. The temperature remains constant, so we are only concerned with volume and pressure. We will use Boyle's Law, which states the volume of a gas is inversely proportional to the pressure. The formula for this law is:
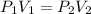
The initial pressure is unknown, but the volume starts at 55.2 liters.
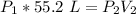
The volume is reduced to 28.8 liters and the pressure is 8.53 atmospheres.
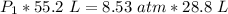
We are solving for the initial pressure, so we must isolate the variable P₁. It is being multiplied by 55.2 liters. The inverse operation of multiplication is division, so we divide both sides of the equation by 55.2 L.
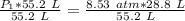
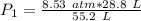
The units of liters (L) cancel.
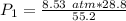
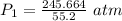
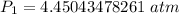
The original measurements of volume and pressure have 3 significant figures, so our answer must have the same. For the number we calculated, that is the hundredths place. The 0 in the thousandths place tells us to leave the 5.
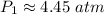
The initial pressure inside the container is approximately 4.45 atmospheres.