Answer:

Explanation:
Quadratic equation:
A quadratic equation, with roots(x-intercepts) at
 and
and
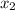 , and leading coefficient a, is given by:
, and leading coefficient a, is given by:

Has x-intercepts of -7 and -1
So
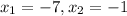 . Thus
. Thus
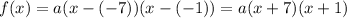
Passes through the point (-4,36).
This means that when
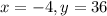 , and we use this to find the leading coefficient.
, and we use this to find the leading coefficient.
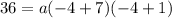
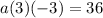
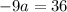

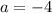
So
