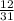Answer:
The probability that they purchased a green or a gray sweater is
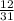
Explanation:
Probability is the greater or lesser possibility of a certain event occurring. In other words, probability establishes a relationship between the number of favorable events and the total number of possible events. Then, the probability of any event A is defined as the quotient between the number of favorable cases (number of cases in which event A may or may not occur) and the total number of possible cases. This is called Laplace's Law.
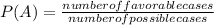
The addition rule is used when you want to know the probability that 2 or more events will occur. The addition rule or addition rule states that if we have an event A and an event B, the probability of event A or event B occurring is calculated as follows:
P(A∪B)= P(A) + P(B) - P(A∩B)
Where:
P (A): probability of event A occurring.
P (B): probability that event B occurs.
P (A⋃B): probability that event A or event B occurs.
P (A⋂B): probability of event A and event B occurring at the same time.
Mutually exclusive events are things that cannot happen at the same time. Then P (A⋂B) = 0. So, P(A∪B)= P(A) + P(B)
In this case, being:
- P(A)= the probability that they purchased a green sweater
- P(B)= the probability that they purchased a gray sweater
- Mutually exclusive events
You know:
- 8 purchased green sweaters
- 4 purchased gray sweaters
- number of possible cases= 12 + 8 + 4+ 7= 21
So:
Then:
P(A∪B)= P(A) + P(B)
P(A∪B)=
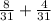
P(A∪B)=
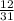
The probability that they purchased a green or a gray sweater is