Answer:
0.01375 = 1.375% probability that the number of lost-time accidents occurring over a period of 10 days will be no more than 2.
Explanation:
We have the mean during the interval, which means that the Poisson distribution is used.
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
Lost-time accidents occur in a company at a mean rate of 0.8 per day.
This means that
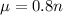 , in which n is the number of days.
, in which n is the number of days.
10 days:
This means that
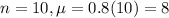
What is the probability that the number of lost-time accidents occurring over a period of 10 days will be no more than 2?
This is:

In which


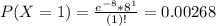
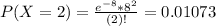
So
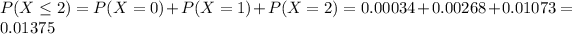
0.01375 = 1.375% probability that the number of lost-time accidents occurring over a period of 10 days will be no more than 2.