Question

A consumer electronics company is comparing the brightness of two different types of picture tubes for use in its television sets. Tube type A has mean brightness of 100 and standard deviation of 16, and tube type B has unknown mean brightness, but the standard deviation is assumed to be identical to that for type A. A random sample of tubes of each type is selected, and is computed. If equals or exceeds , the manufacturer would like to adopt type B for use. The observed difference is . a. What is the probability that exceeds by 3.0 or more if and are equal

Answer 1

The answer is "0.7794".

Explanation:

Please find the complete question in the attached file.

Given:

`\to n_(1)=n_(2)=25\\\\`

Hypotheses:

`\to H_(0):\mu_(B)-\mu_(A)\geq 0\\\\\to H_(a):\mu_(B)-\mu_(A)< 0\\\\`

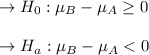
Testing statistics:

`\to z=\frac{(\bar{x}_(B)-\bar{x}_(A))-(\mu_(B)-\mu_(A))}{\sqrt{(\sigma^(2)_(B))/(n_(1))+(\sigma^(2)_(A))/(n_(2))}}=\frac{3.5-(0)}{\sqrt{(16^(2))/(25)+(16^(2))/(25)}}=0.77`

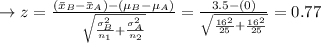
The test is done just so the p-value of a test is

`\to p-value = P(z < 0.77) = 0.7794`

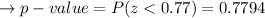
Because the p-value of the management is large, type B can take it.