Question

A random number is selected from the interval [6.35, 10]. Find the probability that the number is within a distance of 0.25 from an even integer. (Answer as a decimal number, and round to 4 decimal places).

Answer 1

Let X be a random number selected from the interval. Then the probability density for the random variable X is

`f_X(x)=\begin{cases}\frac1{10-6.35}=\frac1{3.65}\approx0.2740&\text{if }6.35\le x\le 10\\0&\text{otherwise}\end{cases}`

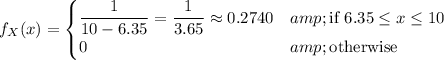
8 and 10 are the only even integers that fit the given criterion (6 is more than 0.25 away from 6.35), so that we're looking to compute

P(|X - 8| < 0.25) + P(|X - 10| < 0.25)

… = P(7.75 < X < 8.25) + P(9.75 < X < 10.25)

… = P(7.75 < X < 8.25) + P(9.75 < X < 10)

(since P(X > 10) = 0)

… = 0.2740 (8.25 - 7.75) + 0.2740 (10 - 9.75)

… = 0.2055