Question

Use the zeros and the labeled point to write the quadratic function represented by the graph

Answer 1

`\sf \boxed{\sf y = -x^2-x +2 }`

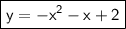
Explanation:

A graph of the quadratic function is given to us and by using the Zeroes , we need to write the function . From the graph , we can sew that , it cuts the x axis on (-2,0) and (1,0) .

Hence , x = -2 and 1 are the zeroes of the function .

In general if we have
`\alpha` and
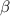`\beta` as the zeroes of the function , then the quadratic function is given by ,

`\sf\longrightarrow\gray{ f(x) = (x -\alpha )(x-\beta) }`

Here the zeroes are -2 and 1 , on substituting the respective values in the formula , we have ,

`\sf\longrightarrow f(x) = \{ x -(-2)\} ( x -1)`

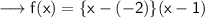
Simplify inside the curly brackets ,

`\sf\longrightarrow f(x) = ( x +2)(x-1)`

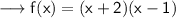
Multiply the two terms ,

`\sf\longrightarrow f(x) = x ( x -1)+2(x-1)`

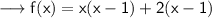
Simplify the brackets ,

`\sf\longrightarrow f(x) = x^2-x +2x -2`

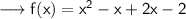
Add the constants and the variables ,

`\sf\longrightarrow f(x) = x^2+x -2`

When the constant of the function is (-1),

`\sf\longrightarrow\boxed{\blue{\sf y = -x^2-x+2}}`

Hence the equation of the function is y = -x² -x + 2 .