Answer:
The number of ways of selecting the team is 26,400 ways.
Explanation:
Given;
total number boys in the gym, b = 10 boys
total number of girls in the gym, g = 12 girls
number of team to be selected, n = 6
If there must equal number of boys and girls in the team, then the team must consist of 3 boys and 3 girls.
Number of ways of choosing 3 boys from the total of 10 =

Number of ways of choosing 3 girls from a total of 12 =

The number of ways of combining the two possibilities;
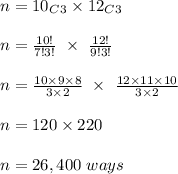
Therefore, the number of ways of selecting the team is 26,400 ways.