Answer:
0.6 = 60% probability that he or she studies on a weeknight.
Explanation:
We solve this question treating these events as Venn probabilities.
I am going to say that:
Probability A: Probability of a student studying on weeknights.
Probability B: Probability of a student studying on weekends.
Forty-two percent of students said they study on weeknights and weekends
This means that
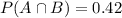
47% said they studied on weekends
This means that
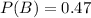
65% said they study either on weeknights or weekends.
This is

If you were to pick one student at random, what is the probability that he or she studies on a weeknight?
This is P(A), and the equation used is:
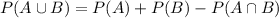
Considering the values we have:

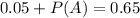

0.6 = 60% probability that he or she studies on a weeknight.