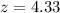Answer:
The z-test statistic for this hypothesis test is
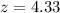
Explanation:
Proportion in 2000:
10 of the 50 men were obese, so:
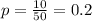
Test if it has increased:
At the null hypothesis, we test if the prevalence of obesity has not increased, that is, the proportion is of 0.2 or less, so:
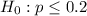
At the alternative hypothesis, we test if this prevalence has increased, that is, the proportion is above 0.2. So
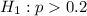
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.2 is tested at the null hypothesis:
This means that

30 out of the 75 men from 2010 were assigned as obese.
This means that
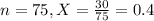
Value of the z-test statistic:

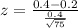
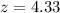
The z-test statistic for this hypothesis test is