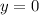Answer:
See explanation
Explanation:
Given
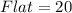
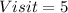
Required
The function to represent x visits
This is calculated as:
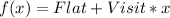
So, we have:

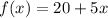
The second question is incomplete; however, I will explain how to calculate the horizontal asymptote of a rational function.
For polynomials with the same degree (i.e. m = n), the horizontal asymptote is calculated by dividing the coefficients of the highest degrees.
e.g.
 ---the degrees of both is 2
---the degrees of both is 2
So, the horizontal asymptote is:
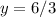
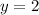
If the numerator has a higher degree, then there is no horizontal asymptote.
If the denominator has a higher degree, then the horizontal asymptote is: