Given:-
- Ross walked 3 m east and 6 m north.
Find:-
- How far is she from the starting point?
solution:-
Ross walked 3 m east and 6 m north.
so her path is a right angle triangle path.
we know that,
in a right angle triangle, According to the Pythagorean theorom,
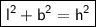
where
- l= legs
- b=base
- h=hypotenuse
According to the question,
Therefore:-
he is
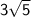 far from the starting point
far from the starting point