Question

Assume that the Poisson distribution applies to the number of births at a particular hospital during a randomly selected day. Assume that the mean number of births per day at this hospital is 13.4224. Find the probability that in a day, there will be at least 1 birth.

Answer 1

0.9999985 = 99.99985% probability that in a day, there will be at least 1 birth.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

Assume that the mean number of births per day at this hospital is 13.4224.

This means that
`\mu = 13.4224`

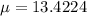
Find the probability that in a day, there will be at least 1 birth.

This is:

`P(X \geq 1) = 1 - P(X = 0)`

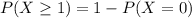
In which

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-13.4224)*13.4224^(0))/((0)!) = 0.0000015`

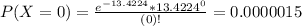
Then

`P(X \geq 1) = 1 - P(X = 0) = 1 - 0.0000015 = 0.9999985`

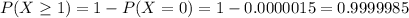
0.9999985 = 99.99985% probability that in a day, there will be at least 1 birth.