Question

A random sample of n1 = 296 voters registered in the state of California showed that 146 voted in the last general election. A random sample of n2 = 215 registered voters in the state of Colorado showed that 127 voted in the most recent general election. Do these data indicate that the population proportion of voter turnout in Colorado is higher than that in California? Use a 5% level of significance.

Answer 1

The p-value of the test is 0.0139 < 0.05, which means that these data indicates that the population proportion of voter turnout in Colorado is higher than that in California.

Explanation:

Before testing the hypothesis, we need to understand the central limit theorem and subtraction of normal variables.

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

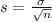For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
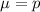`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

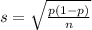
Subtraction between normal variables:

When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.

California:

Sample of 296 voters, 146 voted. This means that:

`p_(Ca) = (146)/(296) = 0.4932`

`s_(Ca) = \sqrt{(0.4932*0.5068)/(296)} = 0.0291`

Colorado:

Sample of 215 voters, 127 voted. This means that:

`p_(Co) = (127)/(215) = 0.5907`

`s_(Co) = \sqrt{(0.5907*0.4093)/(215)} = 0.0335`

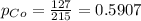
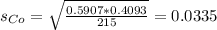
Test if the population proportion of voter turnout in Colorado is higher than that in California:

At the null hypothesis, we test if it is not higher, that is, the subtraction of the proportions is at most 0. So

`H_0: p_(Co) - p_(Ca) \leq 0`

At the alternative hypothesis, we test if it is higher, that is, the subtraction of the proportions is greater than 0. So

`H_1: p_(Co) - p_(Ca) > 0`

The test statistic is:

`z = (X - \mu)/(s)`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, and s is the standard error.

0 is tested at the null hypothesis:

This means that
`\mu = 0`

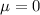
From the two samples:

`X = p_(Co) - p_(Ca) = 0.5907 - 0.4932 =  0.0975`

`s = \sqrt{s_(Co)^2+s_(Ca)^2} = √(0.0291^2+0.0335^2) = 0.0444`

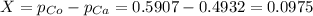
Value of the test statistic:

`z = (X - \mu)/(s)`

`z = (0.0975 - 0)/(0.0444)`

`z = 2.2`

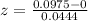
P-value of the test and decision:

The p-value of the test is the probability of finding a difference above 0.0975, which is 1 subtracted by the p-value of z = 2.2.

Looking at the z-table, z = 2.2 has a p-value of 0.9861.

1 - 0.9861 = 0.0139.

The p-value of the test is 0.0139 < 0.05, which means that these data indicates that the population proportion of voter turnout in Colorado is higher than that in California.