Answer:
12.496
Explanation:
a=10 (first term)
r= 1/5 (common ratio)
sum of first five terms
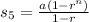
=10{1-⅕⁵} ÷ 1-⅕
=10{1 - 1/3125} ÷ 4/5
=10{3124/3125} ÷ 4/5
=9.9968÷0.8
=12.496.
OR
a+ar+ar²+ar³+ar⁴
=10+(10x⅕)+(10x⅕²)+(10x⅕³)+(10x⅕⁴)
=10+2+0.4+0.08+0.016
=12+0.48+0.016
=12.496