Question

a basketball player pushes down with a force of 50N on a basketball that is indlated to a gage pressure of 8.0x10^4 Pa. What is the diameter of comtact between the ball nad the floor

Answer 1

The diameter of the contact area between the ball and the floor is approximately 28 milimeters.

Step-by-step explanation:

The basketball experiments a normal stress (
`\sigma`), in pascals, due to normal force from the floor (
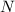`N`). By definition of normal stress, we have the following equation:

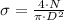`\sigma = (4\cdot N)/(\pi\cdot D^(2))` (1)

Where
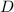`D` is the diameter of the contact area between the ball and the floor, in meters.

Please notice that magnitude of the normal force equals the magnitude of external force given by the basketball player and weight is negligible in comparison with normal and external forces.

If we know that
`N = 50\,N` and
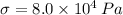`\sigma = 8.0* 10^(4)\,Pa`, then the diameter of the contact area is:

`\sigma = (4\cdot N)/(\pi\cdot D^(2))`

`D^(2) = (4\cdot N)/(\pi\cdot \sigma)`

`D = 2\cdot \sqrt{(N)/(\pi\cdot \sigma) }`

`D = 2\cdot \sqrt{(50\,N)/(\pi\cdot (8* 10^(4)\,Pa)) }`

`D\approx 0.028\,m`
`(28\,mm)`

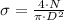
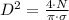
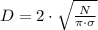
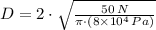
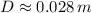
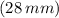
The diameter of the contact area between the ball and the floor is approximately 28 milimeters.