Answer:
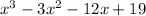 is divisible by
is divisible by
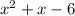 when
when
 is added to it.
is added to it.
Explanation:
Let
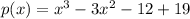 &
&
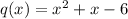
By division algorithm, when p(x) is divided by q(x), the remainder is a linear expression in x
So, let
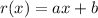 is added to
is added to
 so that
so that
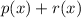 is divisible by
is divisible by
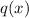
Let,
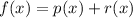
⇒
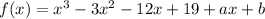
⇒
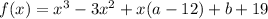
We have,
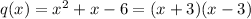
Clearly,
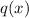 is divisible by
is divisible by
 and
and
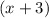
{
 and
and
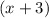 are factors of
are factors of
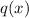 }
}
We have,
 is divisible by
is divisible by
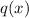
⇒
 and
and
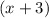 are factors of
are factors of

From factors theorem,
If
 and
and
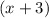 are factors of
are factors of

then
 and
and
 respectively,
respectively,
⇒
 ⇒
⇒

⇒
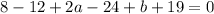
⇒

Similarly,
 ⇒
⇒
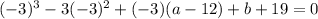
⇒

⇒
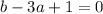
Subtract (1) from (2)
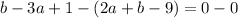
⇒
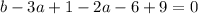
⇒
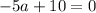 ⇒
⇒
 ⇒
⇒
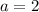
Put
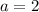 in equation 2
in equation 2
⇒
 ×
×
 ⇒
⇒
 ⇒
⇒
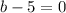 ⇒
⇒
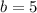
∴
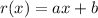 ⇒
⇒

Hence,
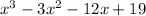 is divisible by
is divisible by
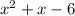 when
when
 is added to it.
is added to it.
Hope this helps...