Question

Given: ∠N ≅ ∠S, line ℓ bisects at Q.

Prove: ∆NQT ≅ ∆SQR

Which statement belongs in Step 4?

Answer 1

angle NQT equals angle STR

Explanation:

You already have two angLes, you just need a side to be able to say the AAS Theorem. The answer is the remaining side to figure that out

Answer 2

A statement belongs in Step 4 include the following: A.
`\overline {TQ}` ≅
`\overline {QR}`.

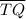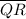In Mathematics and Euclidean Geometry, a segment bisector is a line, line segment, or ray that passes through the midpoint of another line segment and bisects the line into two (2) equal halves or parts.

A midpoint is a point that lies exactly at the middle of two other end points that are located on a straight line segment.

In this context, a two-column proof to proof that triangle NQT is congruent with triangle SQR should be completed as follows;

Statements Reasons__________________________

1. ∠N ≅ ∠S 1. Given

2. ∠NQT ≅ ∠SQR 2. Vertical angles are congruent

3. line ℓ bisects
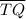`\overline {TQ}` at Q 3. Given

4.
`\overline {TQ}` ≅
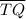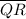`\overline {QR}` 4. Definition of a segment bisector

5. ∆NQT ≅ ∆SQR 5. AAS Theorem