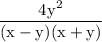Answer:
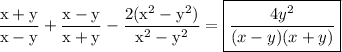
Explanation:
we want to simplify the following
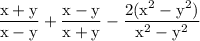
notice that we can reduce the fraction thus do so:
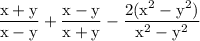
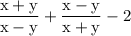
in order to simplify the addition of the algebraic fraction the first step is to figure out the LCM of the denominator and that is (x-y)(x+y) now divide the LCM by the denominator of very fraction and multiply the result by the numerator which yields:
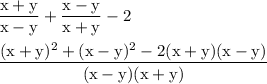
factor using (a-b)²=a²+b²-2ab
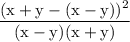
remove parentheses
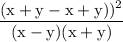
simplify: