Question

1. Find an equation of the line in point-slope form passing through point (-2,5) and parallel to the

line whose equation is 4x - 2y = -5

Answer 1

`\boxed {\boxed {\sf y-5= 2(x+2)}}`

Explanation:

We are asked to find the equation of a line in point-slope form.

As the name of the form describes, we need both a point and the slope. We are given a point, but we have to find the slope.

1. Slope

The line is parallel to the line with the equation of 4x-2y= -5. Parallel lines have the same slope, so once we find the slope of the line with the given equation, we have the slope of the other line whose equation we are finding.

`4x-2y= -5`

We can find the slope by putting the equation into slope-intercept form, or y=mx+b (where m is the slope and b is the y-intercept). We must isolate the variable y. 4x is being added to -2y. The inverse of addition is subtraction, so subtract 4x from both sides.

`4x-4x-2y= -5-4x`

`-2y= -5-4x`

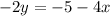
y is being multiplied by -2. The inverse of multiplication is division, so divide both sides by -2.

`-2y/-2=(-5-4x)/-2\\ y= (-5)/(-2) + (-4x)/(-2) \\ y= (5)/(2)+2x`

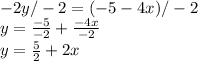
The coefficient of x is the slope, so the slope of the line is 2. Any line that is parallel also has a slope of 2.

2. Point- Slope Equation

Now we have a point and a slope, so we can use the point-slope formula:

`y-y_1=m(x-x_1)`

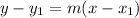
Where m is the slope and (x₁, y₁) is the point.

We know the slope is 2 and the point is (-2,5).

• m=2
• x₁ = -2
• y₁= 5

`y-5=2(x- -2 ) \\\bold {y-5= 2(x+2)}`

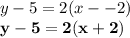
The equation of the line in point-slope form is y-5= 2(x+2)