Answer:
The coefficient of the squared term is 1/25.
Explanation:
We are given that the vertex of a parabola is at (2, -4). We also know that y = -3 when x = -3.
And we want to determine the coefficient of the squared term of the equation.
Since we are given the vertex, we can use the vertex form of the quadratic:
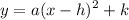
Where (h, k) is the vertex and a is the leading coefficient. The leading coefficient is also the coefficient of the squared term, so we simply need to find the value of a.
Since the vertex is at (2, -4), h = 2 and k = -4. Substitute:
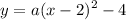
y = -3 when x = -3. Solve for a:
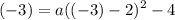
Simplify:
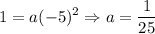
Therefore, our function in vertex form is:
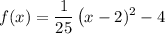
Hence, the coefficient of the squared term is 1/25.